Voronoi and Delaunay cells
Voronoi and Delaunay cells
From now on, consider \(S\) to be a finite set of \(m\) distinct points in \(\mathbb{R}^n\). We denote as \(d(\cdot, \cdot) \colon \mathbb{R}^n \times \mathbb{R}^n \rightarrow \mathbb{R}\) the euclidean metric.
Many definitions and results used throughout this chapter are found and proved in appendix [chapter:app_convex_geometry]. We just require the introduction of the following object.
(Hypersphere) Given a centre \(c \in \mathbb{R}^n\) and a radius \(r > 0\), the corresponding hypersphere is \(\{ x \in \mathbb{R}^n \mid d(x,c) = r\}\).
Voronoi diagrams
Let \(R \subset S\). The Voronoi cell of \(R\), \(V(R)\), is the set
of all points of \(\mathbb{R}^n\) equidistant from all sites in \(R\)
and closer to every site in \(R\) than to any site not in \(R\). That
is,
\(V(R) = \{ x \in \mathbb{R}^n \mid d(x,r_1) = d(x, r_2), \ d(x, r_3) < d(x, q) \ \forall r_1, r_2, r_3 \in R, \ q \in S \setminus R\}\).
Consider 2 distinct points \(p_1, p_2 \in \mathbb{R}^n\). Then, \(V(\{p_1, p_2\})\) is the hyperplane perpendicular to the segment joining both points and equidistant to them. \(V(\{p_1\}), V(\{p_2\})\) are the corresponding half-spaces.
Consider 3 distinct points in the plane \(p_1, p_2, p_3 \in \mathbb{R}^2\). \(V(\{p_1, p_2, p_3\})\) is the single point equidistant to the three of them—the centre of their circumcircle. For \(i \neq j, \ V(\{p_i, p_j\})\) is the semi-infinite line starting at \(V(\{p_1, p_2, p_3\})\) and perpendicular to the segment joining \(p_i, p_j\). \(V(\{p_i\})\) is the corresponding translated cone bounded by these semi-infinite lines.
Consider 4 distinct points in the plane. Then, \(V(\{p_1, p_2, p_3, p_4\})\) is empty unless all 4 points lie on the same circle, in which case it is the centre.
For \(R \subset S\), \(V(R)\) is the relative interior of a polyhedron.
Proof
By [def:polyhedral], we have to show that \(V(R)\) can be written as the relative interior of the intersection of a finite collection of closed half-spaces. In particular, \(d(x, r) < d(x, q) \iff \langle x-r, x-r \rangle < \langle x-q, x-q \rangle \iff - 2 \langle x, r \rangle + \lvert \lvert r\lvert \lvert ^2 < - 2 \langle x, q \rangle + \lvert \lvert q\lvert \lvert ^2 \iff \langle x, b \rangle < \beta\), with \(b = q -r, \ \beta = \frac{\lvert \lvert q\lvert \lvert ^2 - \lvert \lvert r\lvert \lvert ^2}{2}\). Therefore, \(x\) must lie in an open half-space of the hyperplane \(H = \{ x \mid \langle x, b \rangle = \beta \}\). We find all necessary hyperplanes by running over all \(r \in R, \ q \in S \setminus R\). For the equality of distance condition, we can express it as the intersection of two closed halfspaces. Finally, note that \(S\) is finite, and the fact that the inequalities are strict corresponds to taking the relative interior. ◻
As a consequence, all Voronoi cells must be convex.
For a site \(r \in S\), \(V(\{ r \})\) is unbounded \(\iff\) \(r \in \partial \mathrm{conv}(S)\), that is, \(r\) lies on the boundary of the convex hull of \(S\).
Proof
(\(\Rightarrow\) by contrapositive) Suppose \(r \in \mathrm{int}(\mathrm{conv}(S))\). Let \(v\) be an arbitrary unit vector, and construct the ray \(s(t) = r + tv, \ t \geq 0\). Define the sweeping hyperplane \(\perp\) to \(v\) containing \(s(t)\): \(H_t = \{ x \mid \langle x - s(t), v \rangle = 0 \} = \{ x \mid \langle x - r, v \rangle = t \}\). Since \(S\) is compact and \(r\in \mathrm{int}(\mathrm{conv}(S))\), then \(\exists \max_{q \in S \setminus \{r\}} \langle q - r , v\rangle\). Call this value \(t_M\), so for \(t > t_M\), \(H_t\) will never pass through any other site. Let \(q_M \in S \setminus \{r\}\) achieve such a maximum. Then, \(\lvert \lvert s(t) - q_M\lvert \lvert ^2 = t^2 + \lvert \lvert r-q_M\lvert \lvert ^2 - 2 t t_M \Rightarrow d(s(t), q_M)^2 - d(s(t), r)^2 = d(r,q_M)^2 - 2 t t_M\). Therefore, if \(t > \max(t_M, \frac{d(p, q_M)}{2 t_M}) \Rightarrow d(s(t), q_M) < d(s(t), r) \Rightarrow s(t) \not \in V(\{ r\}) \Rightarrow V(\{r\})\) is bounded. We conclude that if \(V(\{r\})\) is unbounded, \(r \not \in \mathrm{int}(\mathrm{conv}(S)) \Rightarrow r \in \partial \mathrm{conv(S)}\).
(\(\Leftarrow\)) Assume \(r \in \partial \mathrm{conv}(S)\) with \(V(\{ r \}) \neq \emptyset\). Then, by [thm:support_hyp] \(\exists\) a supporting hyperplane touching \(\mathrm{conv}(S)\) only at \(r\) such that \(\mathrm{conv}(S)\) lies entirely in one of the corresponding half-spaces. Take its normal outward direction \(v\), and define the ray \(s(t) = r + t v, \ t \geq 0\). Then, \(d(r, s(t)) < d(q, s(t)) \ \forall t \geq 0, q \in S \setminus \{ r\}\). Thus, \(s(t) \in V(\{ r \}) \ \forall t \geq 0\), and since \(s(t)\) is unbounded, \(V(\{ r \})\) must also be unbounded. ◻
Then, since bounded voronoi cells are bounded polyhedra, they must also be polytopes (see [sec:polyh]), so they have a finite representation in the sense of [def:polytope]. That is, bounded voronoi cells are the convex hull of a finite number of vertices.
The Voronoi diagram of \(S\), \(V_S\), is the collection of all non-empty Voronoi cells \(V(R)\) for \(R \subset S\).
\(V_S\) is a cell complex (in the sense of [def:cell_complex]) that partitions \(\mathbb{R}^n\).
Proof
We first show that the Voronoi cells are pairwise disjoint. Let
\(R, R' \subset S, R \neq R'\). Assume
\(V(R) \cap V(R') \neq \emptyset\). Take \(x \in V(R) \cap V(R')\).
Since \(x \in V(R)\),
\(d(x, r) < d(x, r')\ \forall r \in R, r' \in R'\). However, we must
also have \(d(x, r') < d(x, r)\ \forall r' \in R', r \in R\), which is a
contradiction. Therefore, \(V(R) \cap V(R') = \emptyset\) and the
Voronoi cells are all pairwise disjoint.
We now wish to show that every face of every cell of \(V_S\) is also in
\(V_S\). Take \(V(R)\) for some \(R \subset S\). Any face of \(V(R)\)
corresponds to the set obtained by tightening some of the inequalities
\(d(x,r) < d(x,q) \rightarrow d(x,r) = d(x,q)\) \(\forall r \in R\) for
some \(q \in S \setminus R\). Therefore, such a face corresponds to
\(V(R \cup q)\) for some
\(q = \{q_1, \ldots, q_k\} \subset S \setminus R\), so it must also
belong to \(V_S\).
To see that it partitions \(\mathbb{R}^n\), we show that
\(\forall x \in \mathbb{R}^n\), \(x \in V(R)\) for some \(R \subset S\).
It suffices to find the site \(r \in R\) that is closest to \(x\), and
by definition \(x \in V(\{r\})\). If \(x\) is equidistant to more than
one site, gather them in a set \(\{r_1, \ldots, r_k\}\) and then again
\(x \in V(\{ r_1, \ldots, r_k\})\). ◻
Therefore, any point \(x \in \mathbb{R}^n\) lies in \(V(R)\) for some \(R \subset S\), although \(R\) may consist of more than a single point. However, for an arbitrary \(R \subset S\), \(V(R)\) may be empty. This happens if any of the conditions of the definition cannot be satisfied.
Delaunay triangulations
If \(R \subset S\) and \(V(R) \neq \emptyset\), the Delaunay cell \(D(R)\) is defined as \(\mathrm{cell}(R)\). That is, \(D(R) = \mathrm{cell}(R) = \mathrm{ri}(\mathrm{conv}(R))\) (see [def:cell]).
Note that by definition, a Delaunay cell is convex. The next is a very important property characterising such cells.
(Empty sphere property) For \(R \subset S\), \(D(R)\) is a Delaunay cell \(\iff\) \(\exists\) a circumscribed hypersphere of \(R\) that contains no site of \(S \setminus R\) in its interior.
Proof
\((\Rightarrow)\) Assume \(D(R)\) is a Delaunay cell, so \(V(R) \neq \emptyset\). Take \(x \in V(R)\). Then \(d(x, r_i) = d(x, r_j) \ \forall r_i, r_j \in R\). Construct the hypersphere centred at \(x\) with radius \(d(x, r_i)\). This is a circumscribed hypersphere of \(R\), since all sites of \(R\) belong to it. By the second property of \(V(R)\), \(d(x, r_k) < d(x, r_l), \forall r_k \in R, r_l \in S \setminus R\), so all sites of \(S \setminus R\) lie in its exterior.
\((\Leftarrow)\) Conversely, assume \(\exists\) such a hypersphere of \(R\). By definition, its center belongs to \(V(R) \Rightarrow V(R) \neq \emptyset\), so \(D(R)\) is well defined. ◻
It is important to note that a Delaunay cell is not necessarily a simplex. This can happen in degenerate cases as we discuss in the last section. Therefore, \(D_S\) need not be a proper triangulation (in the sense of [def:proper_triang]).
Consider 4 cocircular points in the plane. Then, \(V(\{p_1, p_2, p_3, p_4 \})\) is the center of the circle, and \(D(\{r_1, r_2, r_3, r_4\})\) is a quadrilateral (which is not a simplex).
The Delaunay triangulation of \(S\), \(D_S\), is the collection of Delaunay cells \(D(R)\) for \(R \subset S\) and \(V(R) \neq \emptyset\).
\(D_S\) is a triangulation of \(S\) (in the sense of [def:triangulation]).
Proof
-
We first prove that Delaunay cells are pairwise disjoint. Consider \(R, R' \subset S, \ R \neq R'\), having well defined Delaunay cells. If \(R' \subset R\), then \(\mathrm{conv}(R')\) is a face of \(\mathrm{conv}(R)\), and their relative interiors must be disjoint by [cor:face_ri]. If \(R \cap R' \neq \emptyset\) but \(R' \not\subset R\) and \(R \not \subset R'\), we can construct a hyperplane intersecting \(R \cap R'\) separating (non-strictly) \(D(R)\) and \(D(R')\) ([thm:hyperplane_sep]). Finally, if \(R \cap R' = \emptyset\), consider the corresponding circumscribed hyperspheres \(C, C'\) satisfying the empty sphere property, and we have two cases. If \(C \cap C' = \emptyset \Rightarrow D(R) \cap D(R') = \emptyset\). Otherwise, construct a hyperplane passing through \(C \cap C'\) strictly separating \(R\) and \(R'\).
-
We now show that every face of a Delaunay cell \(D(R)\) is also a Delaunay cell. Any face of \(D(R)\), different from \(D(R)\) itself, is precisely \(\mathrm{cell}(R')\) with \(R' = R \cap H\) for some hyperplane \(H\) supporting \(\mathrm{conv}(R)\). An empty circumscribed sphere to \(R\) can be slightly perturbed to be an empty circumscribed sphere of \(R'\), so \(\mathrm{cell}(R')\) is also a Delaunay cell by [lemma:circum_sph].
-
Thus far we have proved that \(D_S\) is a cell complex. We now show that \(\mathrm{conv}(S) = \bigcup_{R \subset S} D(R)\). Consider \(x \in \mathrm{conv}(S)\). By Carathéodory’s theorem [thm:caratheodory], \(\exists R \subset S\) such that \(x \in \mathrm{conv}(R)\) with \(\lvert R\lvert \leq n+1\). Take \(R\) as the minimal such set, that is, the one with the least elements s.t. \(x \in \mathrm{ri}(\mathrm{conv}(R))\). (a) If \(\lvert R\lvert = n+1\), then \(\exists ! C\) circumscribed hypersphere to \(R\). If \(\exists q \in S \setminus R\) that lies inside \(C\), we can replace a point of \(R\) by \(q\), such that \(x\) is still in its convex hull but the hypersphere is smaller. Repeat until there is no such point inside \(C\), so by [lemma:circum_sph], \(x \in D(R)\). (b) If \(\lvert R\lvert < n+1\), a similar construction is done on \(\mathrm{aff}(R)\), resulting in a Delaunay cell of smaller dimension. Therefore, \(\mathrm{conv}(S) \subset \bigcup_{R \subset S} D(R)\). Note that \(\bigcup_{R \subset S} D(R) \subset \mathrm{conv}(S)\) is true by definition.
-
As shown, every face of every cell must belong to \(D_S\), in particular 0-dimensional faces which correspond to the vertices in \(S\). Conversely, assume that there exists a point \(p \in S\) that is not a vertex in \(D_S\). Thus, it must lie strictly inside some \(D(R)\subset D_S\), violating the empty sphere condition and resulting in a contradiction. Therefore, the vertices of \(D_S\) are precisely \(S\).
◻
Finally, it is useful to characterise Delaunay cells locally.
Two opposite \(n\)-cells \(\mathrm{cell}(R)\) and \(\mathrm{cell}(R')\) are locally Delaunay if \(R, R'\) have corresponding circumscribed hyperspheres \(C, C'\) such that \(R \setminus R'\) lies outside \(C'\) (equivalently, \(R' \setminus R\) lies outside \(C\)).
A triangulation is Delaunay \(\iff\) all \(n\)-cells are locally Delaunay.
Proof
(\(\Rightarrow\)) If a triangulation is Delaunay, then by the empty sphere property, all \(n\)-cells must be locally Delaunay. (\(\Leftarrow\)) Select an \(n\)-cell \(D(R)\). We will prove that any \(s \in S \setminus R\) lies outside of the circumscribed hypersphere of \(R\). Select \(r \in \mathrm{int}(\mathrm{conv}(R)) = D(R)\) such that the line segment \(\overline{rs}\) avoids all \(k\)-cells for \(k \leq n-2\) and intersects \((n-1)\)-cells transversally. We may always find such an \(r\) since the triangulation is finite and the set of “bad” directions is a finite union of lower-dimensional subsets of the unit sphere of measure zero. This generates a sequence \(N_0, F_1, N_1, \ldots, F_k, N_k\) where \(N_i\) are the \(n\)-cells and \(F_i\) the \((n-1)\)-cells (facets) that \(\overline{rs}\) intersects until it arrives to \(s\). Denote by \(C_i\) the circumscribed hypersphere of \(N_i\). We will do an inverse induction on \(i = k, \ldots, 0\). For the base case consider \(N_k\), note that there is a hyperplane passing through \(F_k\) separating \(s\) from \(N_{k-1}\) and \(s\) must lie outside of \(C_{k-1}\) (locally Delaunay). The induction hypothesis is that \(s\) lies outside of \(C_i\). Now, consider \(N_{i-1}\). The hyperplane passing through \(F_i\) separates the only vertex of \(N_i\) not shared by \(N_{i-1}\), and it must lie outside of \(C_{i-1}\) (locally Delaunay). Since the intersection of \(\overline{rs}\) with \(F_{i}\) is transversal, \(s\) must also lie on the same side of the plane, and by the induction hypothesis, it must also be outside of \(C_{i-1}\). Thus, we have proved that \(s \not \in C_0\), so all sites \(s \in S \setminus R\) are outside the circumscribed hypersphere of \(R\). ◻
Duality
The following theorem establishes a duality relationship between \(V_S\) and \(D_S\).
\(V_S\) and \(D_S\) are dual. That is, for \(R, R' \subset S\), \(V(R)\) is a face of \(V(R')\) \(\iff\) \(D(R')\) is a face of \(D(R)\).
The proof makes use of many constructions developed in the proofs of [thm:vor_complex] and [thm:del_triang]
Proof
Suppose \(V(R), V(R')\) are distinct Voronoi cells, so \(D(R), D(R')\) are distinct Delaunay cells. Then, \(V(R')\) is a face of \(V(R)\) \(\iff\) some of the inequalities defining \(V(R)\) are tightened to equalities \(\iff R' = R \cup q\) for some \(q \subset S \setminus R\) \(\iff R = R' \cap H\) for some hyperplane \(H\) containing \(q\) that supports the convex hull of \(R'\) \(\iff D(R)\) is a face of \(D(R')\). ◻

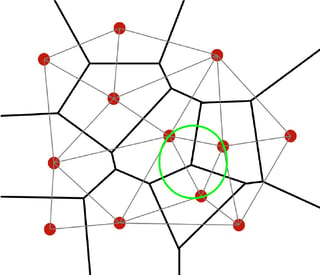
Dimensionality and degeneracies
If \(V(R) \neq \emptyset\), \(\mathrm{dim}(V(R)) = n - \mathrm{dim}(\mathrm{conv}(R))\).
Proof
Note \(V(R)\) is a relatively open subset of the affine set \(M = \{ x \mid d(x, r_i) = d(x, r_j) \ \forall r_i, r_j \in R\}\), so \(dim(V(R)) = dim(M)\). Note \(d(x, r_i) = d(x, r_j) \ \forall r_i, r_j \in R \iff \langle x, r_i - r_1 \rangle = \frac{1}{2}( \lvert \lvert r_i\lvert \lvert ^2 - \lvert \lvert r_1\lvert \lvert ^2) \ \forall r_i \neq r_1 \in R\), so \(x\) is the solution set to the system \(\mathbf{A} x = b\), with \(\mathbf{A}\) having \(r_i - r_1\) as columns. Then, \(\mathrm{dim}(M) = n - \mathrm{rank}(\mathbf{A})\). Note that by definition ([def:conv_dim]) \(\mathrm{dim}(\mathrm{conv}(R)) = \mathrm{dim}(\mathrm{aff}(R))\), and as developed in [sec:affine], \(\mathrm{dim}(\mathrm{aff}(R)) = \mathrm{dim}(\mathrm{span}(\{ r_2-r_1, \ldots, r_m-r_1\})) = \mathrm{rank}(\mathbf{A})\). ◻
If \(V(R) \neq \emptyset\), \(\mathrm{dim}(V(R)) \geq n - \lvert R\lvert + 1\) and \(\mathrm{dim}(D(R)) \leq \lvert R\lvert - 1\).
Proof
Note that \(\mathrm{dim}(D(R)) = \mathrm{dim}(\mathrm{conv}(R)) = \mathrm{dim}(\mathrm{aff}((R)) \leq \lvert R\lvert - 1\) (see [sec:affine]) and use [prop:dim_voronoi]. ◻
If \(V(R) \neq \emptyset\), \(\mathrm{dim}(V(R)) + \mathrm{dim}(D(R)) = n\).
Proof
Note that \(\mathrm{dim}(D(R)) = \mathrm{dim}(\mathrm{ri}(\mathrm{conv}(R))) = \mathrm{dim}(\mathrm{conv}(R))\) and simply use [prop:dim_voronoi]. ◻
If \(V(R) \neq \emptyset\) and \(\mathrm{dim}(V(R)) > n - \lvert R\lvert + 1\) (or \(\mathrm{dim}(D(R)) < \lvert R\lvert -1\)), then \(V(R)\) and \(D(R)\) are degenerate.
If the cells are degenerate, the previous propositions imply that the sites in \(R\) are not affinely independent. That is, all sites lie on a common affine set \(M\) with \(\mathrm{dim}(M) < \lvert R\lvert - 1\). Furthermore, since \(D(R)\) is well defined, all sites must lie on a common circumscribed hypersphere; otherwise the empty sphere condition would not be satisfied. Thus, if \(\lvert R\lvert > n +1\) and \(V(R) \neq \emptyset\), the sites must lie on a common circumscribed hypersphere, and the corresponding cells are degenerate.
If \(\lvert R\lvert = 1, 2, 3\), then \(V(R)\) and \(D(R)\) are never degenerate.
Proof
For \(\lvert R\lvert = 1\), the condition \(\mathrm{dim}(V(R)) > n - \lvert R\lvert + 1 = n\) can never be satisfied, since the maximum dimension is \(n\). For \(\lvert R\lvert = 2\), \(R = \{ r_1, r_2\}\). If \(V(R) \neq \emptyset\), \(V(R)\) must be a relatively open subset of the 1-dimensional affine space \(d(x, r_1) = d(x, r_2)\), so \(\mathrm{dim}(V(R)) \leq 1\). In fact, \(\mathrm{dim}(V(R)) \leq \min \{n-1, 1\}\) (if \(n=1\), then \(V(\{r_1, r_2\})\) must be a single point), so \(\mathrm{dim}(V(R)) \not > n - 1\). For \(\lvert R\lvert = 3\), note that the sites cannot lie in a line and in a hypersphere simultenously, so degeneracy is not possible. ◻
\(S\) is in general position if no \(n+2\) points lie on a common hypersphere and every subset of at most \(n+1\) elements is affinely independent.
If \(S\) is in general position, then no cell is degenerate. In such a case, all Delaunay cells are simplexes, so \(D_S\) is a proper triangulation. Additionally, all Voronoi cells have dimension \(n-(\lvert R\lvert -1)\) and all Delaunay cells have dimension \(\lvert R\lvert -1\).
References
- S. Fortune. “VORONOI DIAGRAMS and DELAUNAY TRIANGULATIONS”