Montecarlo simulation of an Isobaric and Isothermal Lennard-Jones system
Partition function
The partition function \(Q(N,P,T)\) for a system with constant number of particles \(N\), pressure \(P\) and temperature \(T\) is
\[Q(N,P,T) = \frac{\beta P}{\lambda ^{3N}N!}\int \mathrm{d}V V^N e^{-\beta PV} \int { \mathrm{d}\vec{s}}^N e^{-\beta U(\vec{s}^N;L)} = \beta P\int \mathrm{d}V e^{-\beta PV} Q_{\text{can}} (N,V,T).\]We assume that the particles are in a cube with side length \(L = V^{\frac{1}{3}}\). Note that it can be expressed in terms of an integral over volume by appropriately weighting the canonical ensemble’s partition function \(Q_{\text{can}}(N,V,T)\), plus an extra factor \(\beta P\) necessary to make it dimensionless.
Finally, we consider Lennard-Jones interactions for the energy \(U(\vec{s}^N ; L)\).
Montecarlo sampling
Configuration space can be parametrized by \(\{ \log{V}, \vec{s}^N\} = \{ \log{V}, \vec{s}_1, \ldots, \vec{s}_N\}\). It is easy to obtain that the probability density of being in a particular state \(\{ \log{V}, \vec{s}^N\}\) is
\[N(\{\log{V}, \vec{s}^N\}) = V^{N+1} e^{-\beta P V} e^{-\beta U(\vec{s}^N; L)} = e^{- \beta [ PV + U - \frac{N+1}{\beta} \log{V}]}.\]Then, according to the Metropolis algorithm, the acceptance probability of a trial move from configuration \(o \to n\) is
\[\text{acc}(o \to n) = \min\left\{1, \frac{N(n)}{N(o)}\right\} = \min\left\{1, \ e^{- \beta [ P(V_n - V_o) + (U_n-U_o) - \frac{N+1}{\beta} \log{(\frac{V_n}{V_o})}]} \right\}.\]The sampling allows us to find, for each \(N, P, T\):
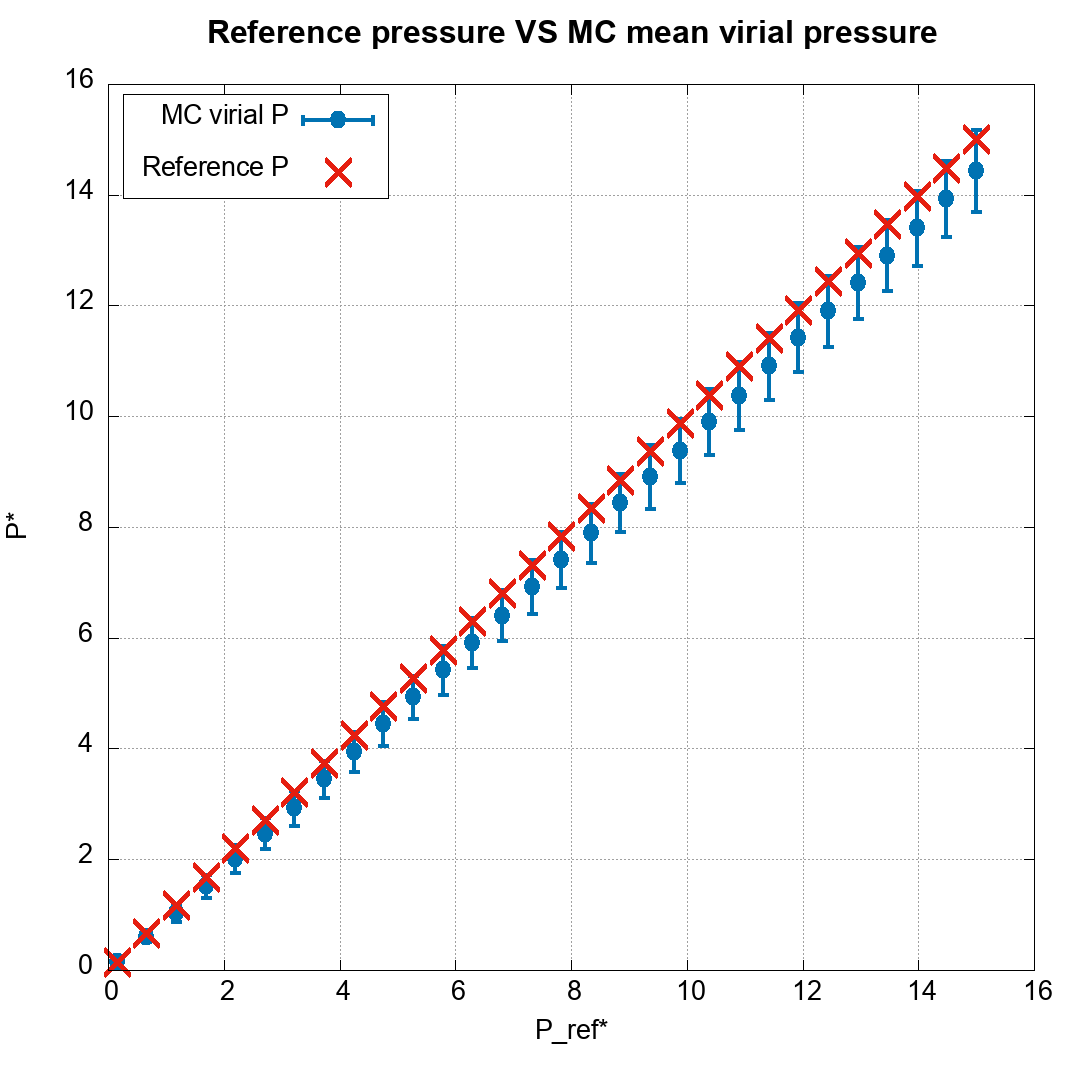
- The virial pressure to compare with the imposed pressure.
- The average density and volume.
- The average energy.
- The radial distribution function.
This has been implemented in FORTRAN.
Some results
The following are the results for a system of Argon particles, characterized by the following parameters:
\[m = 39.948 \ \text{uma}, \quad \varepsilon / k_B = 119.8 \text{K}, \quad \sigma = 3.405 \text{A}\]The pressure is varied between 0.00613 GPa (0.15 in reduced units) and 0.604 GPa (15 in reduced units) in 30 uniformly distributed steps. The temperature is fixed at 239.6 K (2 in reduced units). Each macroscopic configuration of (N, P, T) is sampled every 500 MC steps for a total of 2000 samples.