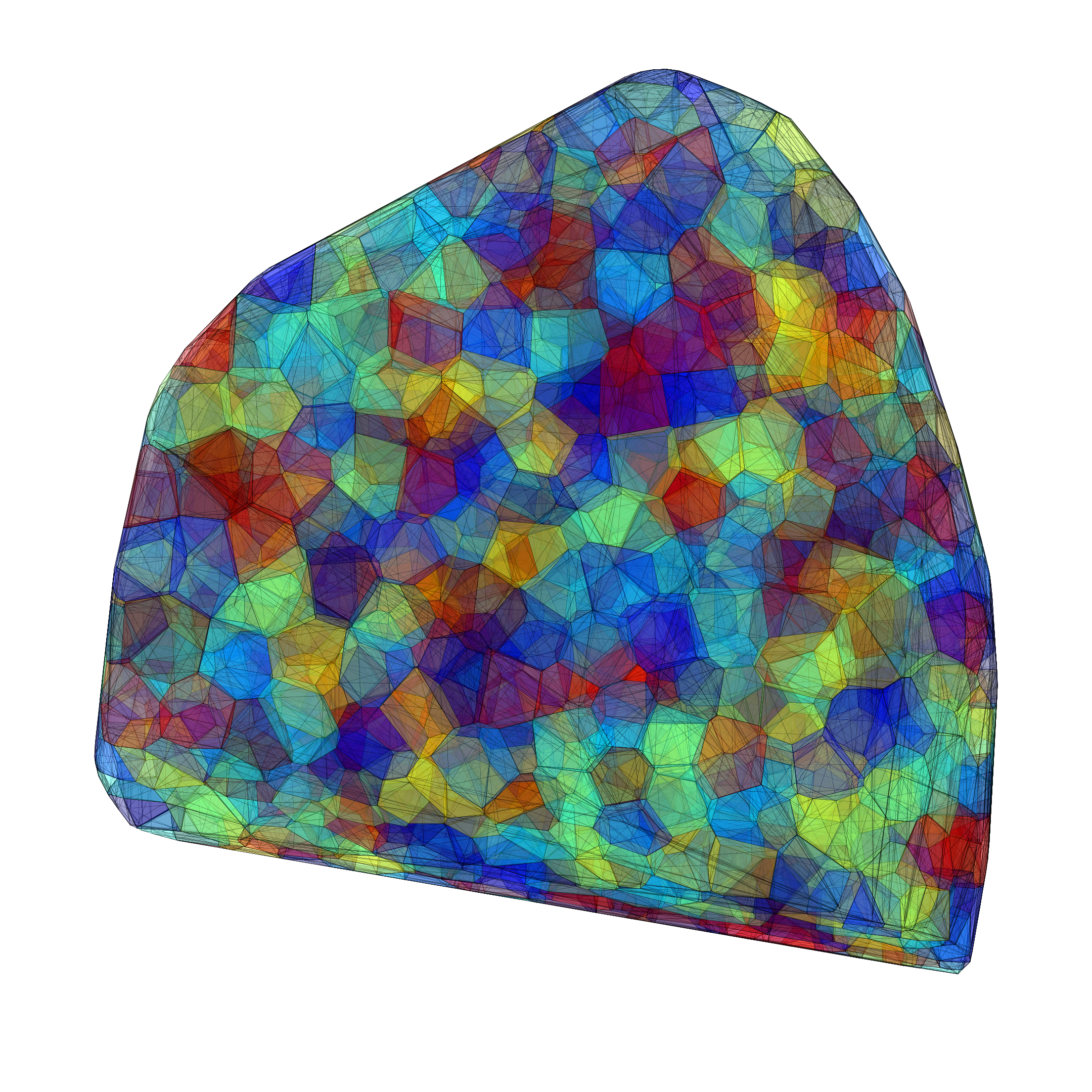
Robust Delaunay triangulation
Given a set of seeds, to find its Voronoi diagram we first construct the associated Delaunay triangulation. To do so, we have implemented in C the algorithm described in the paper Computing the 3D Voronoi Diagram Robustly: An Easy Explanation by Hugo Ledoux (link).
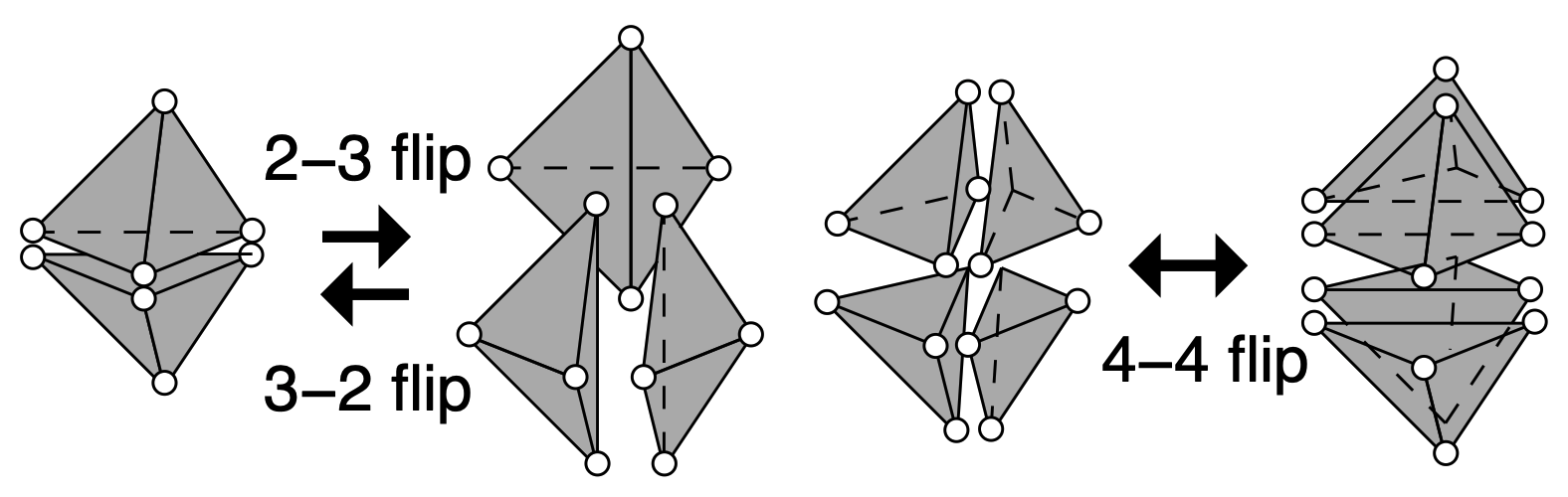
The idea of the algorithm is to iteratively add each seed and at each step restore local Delaunayness by using Pachner flips (or bistellar flips).
When the Delaunay triangulation is constructed, extracting the corresponding Voronoi diagram is trivial due to the duality relationships between the Delaunay and Voronoi constructions. However, the resulting Voronoi diagram is unbounded.
Bounding polyhedron
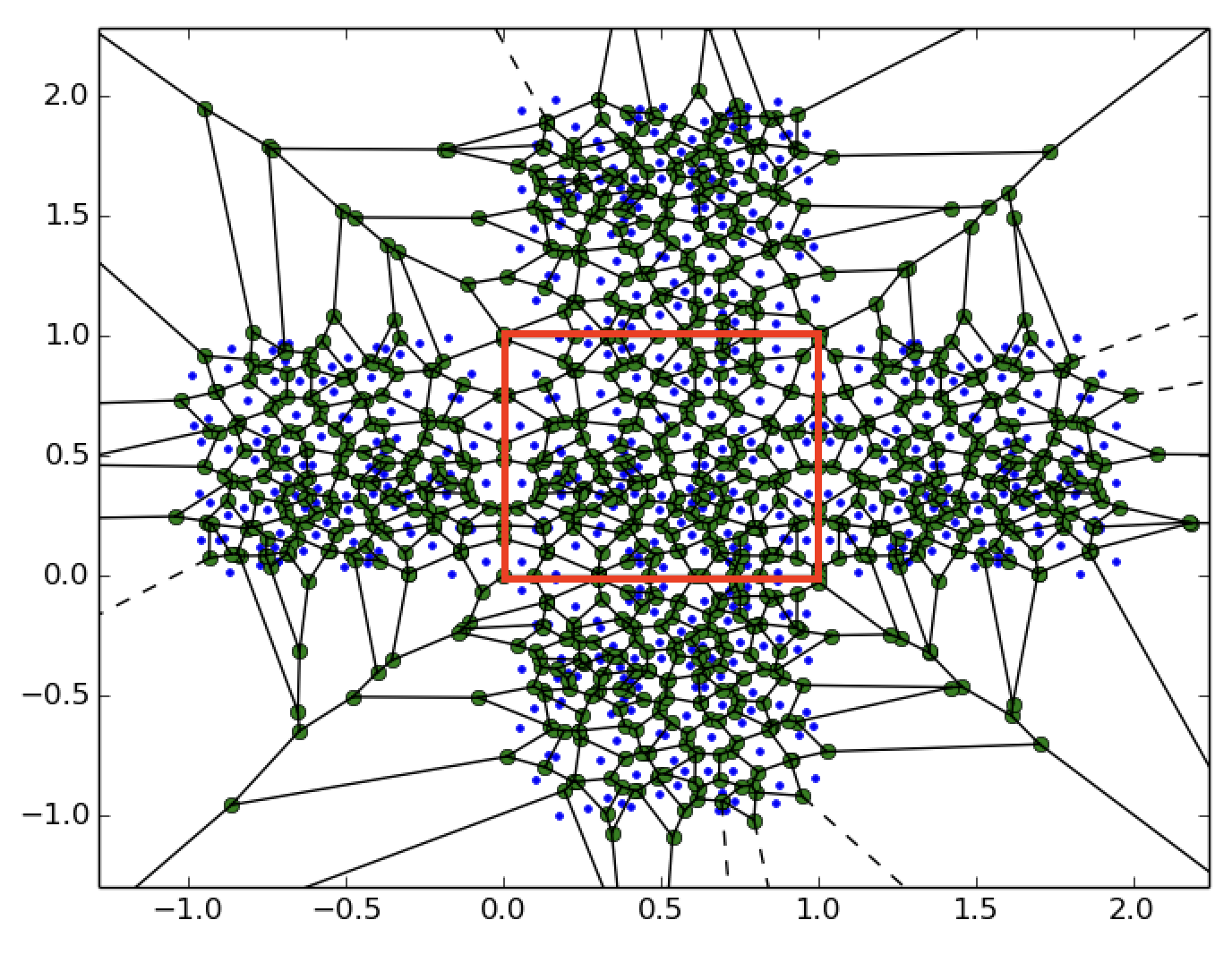
In order to bound the diagram appropriately with an arbitrary polyhedron, we use a mirroring appraoch. The idea is to enlarge the set of seeds by mirroring the necessary sites accross each face of the bounding polyehdron. Then, the Delaunay triangulation of this extended set of seeds is computed. Finally, we extract the dual Voronoi cells in the interior of the polyhedron, which will be naturally bounded.
The next figure (from this StackOverflow discussion, comment by Flabetvibes) shows an example of this principle in the plane, with the goal of bounding the cells corresponding to the points inside the red box.
Example in lung geometry
This code has been used to construct secondary pulmonary lobules inside a lung geometry. By playing with the distribution of seeds inside the lung, we can obtain different morphologies and distributions of lobule volumes.